|
PREDICTING POKER HANDS WITH NEURAL NETWORKS An example of a multivariate data type classification problem using Neuroph by Nikola Ivanić, Faculty of Organisation Sciences, University of Belgrade an experiment for Intelligent Systems course
Introduction In this experiment it will be shown how to solve classification problem using neural networks and Neuroph Studio software. It will be shown how we tried several architectures and determined which ones represent a good solution to the problem, and which ones do not. There is a number of advantages to using neural networks - they are data driven, they are self-adaptive, they can approximate any function - linear as well as non-linear (which is quite important in this case because groups often cannot be divided by linear functions). Neural networks classify objects rather simply - they take data as input, derive rules based on those data, and make decisons.
Introducing the problem The objective is to train the neural network to predict which poker hand do we have based on cards we give as input attributes. First thing we need for that, is to have a data set. A data set found on http://archive.ics.uci.edu/ml/datasets/Poker+Hand will be used.The database was obtained from the Carleton University, Department of Computer Science Intelligent Systems Research Unit, Canada. The data set contains more than 25000 instances but because of software limitation we worked with shorter version of 1003 instances. Each record is an example of a hand consisting of five playing cards drawn from a standard deck of 52. Each card is described using two attributes (suit and rank), for a total of 10 predictive attributes. There is one Class attribute that describes the "Poker Hand". The order of cards is important. The characteristics that are used in the prediction process are: 1) S1 "Suit of card #1" Each attribute will be described with binary sets(0 and 1). There are four different card suits(Hearts,Spades,Diamonds,Clubs) so it will be four binary sets to describe them. There are 13 different cards in every suit and they will get their own binary sets with 13 values to describe them:
There are 10 possible poker hands depending which 5 cards we have so we need to give matching binary set for every poker hand :
The data set can be dowloaded here, however, it can not be inserted in Neuroph in its original form. For it to be able to help us with this classification problem, we need to change the data first in the way it is described above. The type of neural network that will be used in this experiment is multi layer perceptron with backpropagation.
Prodecure of training a neural network In order to train a neural network, there are five steps to be made: 1. Adjustments of dataset(explained above) 2. Create a Neuroph project 3. Create a training set 4. Create a neural network 5. Train the network 6. Test the network to make sure that it is trained properly
Creating a new Neuroph project First, a new Neuroph projects needs to be created by clicking on the 'File' menu, and then 'New project'.It should be selected Neuroph Project and clicked Next. The project will be called 'Neuroph Project' and with clicking on Finish button new project is created and saved in selected Project Location .
New project is created and it will appear in the 'Projects' window, in the top left corner of Neuroph Studio.
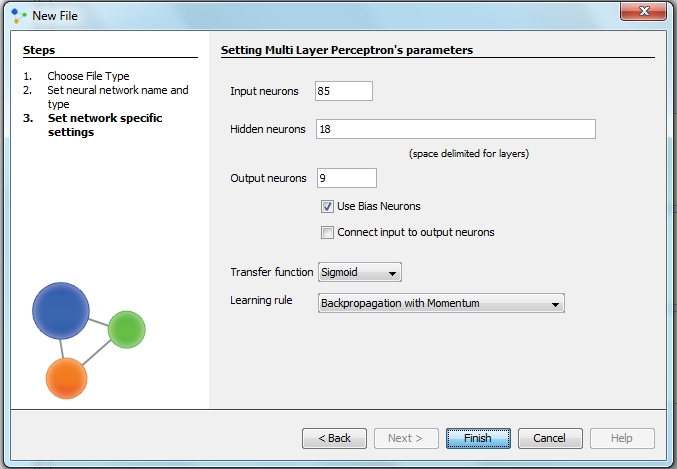
Creating a training set Next, we need to create a new training set by right-clicking on our project, and selecting 'New', and 'Training set'. We give it a name, and then set the parameters. The type is chosen to be 'Supervised' training , because we want to minimize the error of prediction through an iterative procedure. Supervised training is accomplished by giving the neural network a set of sample data along with the anticipated outputs from each of these samples. That sample data will be our data set. Supervised training is the most common way of neural network training. As supervised training proceeds, the neural network is taken through a number of iterations, until the output of the neural network matches the anticipated output, with a reasonably small rate of error. Error rate we find to be appropriate to make the network well trained is set just before the training starts. Usually, that number will be around 0.01. Next, we set the number of input and the number of outputs. In our case we will have 85 inputs and 9 outputs. We have 85 inputs because of 5 cards in hand and every card have suit(set of 4 values) and rank(set of 13 values) ---> 5*(4+13)=85; and we have 9 outputs as we have set of 9 values for describing a poker hand.
After clicking next, we need to edit training set table. In this case, we will not write the table ourselves, but rather click a 'Load from file', to select a file from which the table will be loaded. We click on 'Choose file', find the file with data we need, and then select a values separator. In this case, it is tab because of adjustment explained earlier(those have been done in Office Excell), but it can also be a space, comma, or semicolon.Then, we click 'Next', and a window that represents our table of data will appear. Because of very large amount of input and output values, we can't notice that everything is in order, but there are really 85 input and 9 output columns, every input have 0 or 1 as a value, and we can now click on 'Finish'.
Our newly created training set will appear in the 'Projects' window. After completing this, everything is ready for the creation of neural networks. We will create several neural networks, all with different sets of parameters, and determine which is the best solution for our problem by testing them. This is the reason why there will be several options for steps 4, 5 and 6.
Training attempts 1 and 2Creating a neural network We will create our first neural network by right-clicking our project in the 'Projects' window, and then clicking 'New' and 'Neural Network'. A wizard will appear, where we will set the name and the type of the network. Multi Layer Perceptron will be selected. Multi layer perceptron is the most widely studied and used neural network classifier. It is capable of modeling complex functions, it is robust (good at ignoring irrelevant inputs and noise) ,and can adapt its weights and/or topology in response to environment changes. Another reason we will use this type of perceptron is simply because it is very easy to use - it implements black-box point of view, and can be used with few knowledge about the relationship of the function to be modeled.
When we have selected the type of the network, we can click 'Next'. A new window will appear, where we will set some more parameters that are characteristic for multi layer perceptron. The number of input and output neuron is the same as the number of inputs and outputs in the training set. However, now we have to select the number of hidden layers, and the number of neurons in each layer. Guided by the rule that problems that require two hidden layers are rarely encountered (and that there is currently no theoretical reason to use neural networks with any more than two hidden layers), we will decide for only one layer. As for the number of units in the layer, since it is known that one should only use as much neurons as it is needed to solve the problem, we will choose as little as we can for the first experiment - only five. Networks with many hidden neurons can represent functions with any kind of shape, but this flexibility can cause the network to learn the noise in the data. This is called 'overtraining'. We have checked 'Use Bias Neurons', and chosen sigmoid transfer function (because the range of our data is 0-1, had it been -1 to 1, we would check 'Tanh'). As a learning rule we have chosen 'Backpropagation with Momentum'. This learning rule will be used in all the networks we create, because backpropagation is most commonly used technique and is most suited for this type of problem. In this method, the objects in the training set are given to the network one by one in random order and the regression coefficients are updated each time in order to make the current prediction error as small as it can be. This process continues until convergence of the regression coefficients. Also, we have chosen to add an extra term, momentum, to the standard backpropagation formulae in order to improve the efficiency of the algorithm.
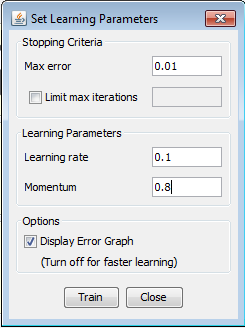
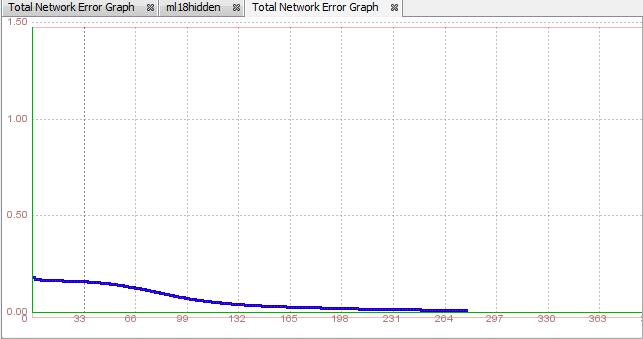
Next, we click 'Finish', and the first neural network which we will test is completed. Training the neural network Now we need to train the network using the training set we have created. We select the training set and click 'Train'. A new window will open, where we need to set the learning parameters. The maximum error will be 0.01, learning rate 0.2 and momentum will be 0.7. Learning rate is basically the size of the 'steps' the algorithm will take when minimizing the error function in an iterative process. We click 'Train' and see what happens. A graph will appear where we can see how the error is changing in every iteration. We wanted to train our network with the smallest possible error so we used for Max error 0.01 but, the error haven't drop below 0.05 after 8000 iterations so we couldn't train our network with that max value. That is maybe expected because of small learning rate but although we tried with learning rate 0.5, we had same results. Obviously, the main reason for those results is small amount of hidden neurons, only five !
Unfortunately, we couldn't test our network , but we could make different one , with more hidden neurons which will help to solve our problem.
Training attempts 3 and 4Creating a neural network In our second attempt to create the optimal architecture of neural network for the problem, we will pay more attention to the number of neurons we choose to have in the hidden layer. Now we will use 10 hidden neurons in our second training attempt.
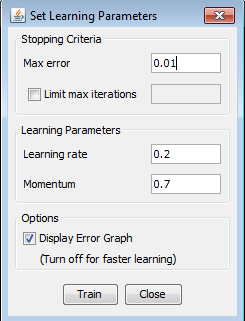
Step 5.2 Training the network Now, the neural network that will be used as our second solution to the problem has been created. Just like the previous neural network, we will train this one with the training set we created before. We selected our training set , clicked Train and we filled in same parameters for learning. We do not limit the maximum number of iterations. After we click 'Train', the iteration process starts. After the initial downfall, error function begins to rise after 1500 iterations, and again we are not able to train the network using these parameters.
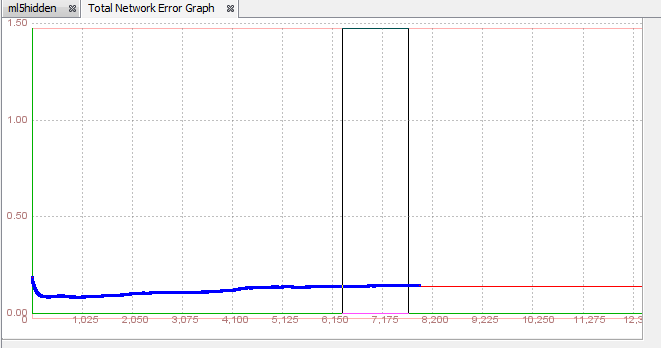
Maybe our max error for this kind of network with 10 hidden neurons has to be a little bit bigger than 0.01, so in our second attempt with this network we used max error of 0.03. We had these results :
As you can see from the Graph, our training finished after 134 iterations, error has dropped below 0.03 and now we can test our network.
Testing the network We click 'Test' and wait for the results.The test results will show the difference between the guess made by the network and the correct value for the output. The test showed that total mean square is 0.00738. Now we need to examine all the individual errors for every single instance and check if there are any extreme values.
Training attempt 5Creating and training the network We can try to change the number of hidden neurons. This time, we will create the network with 12 hidden neurons. Because of 2 neurons more than last time, now we will use 0.02 value as max error instead of 0.03. Learning rate and momentum for now , will be the same.
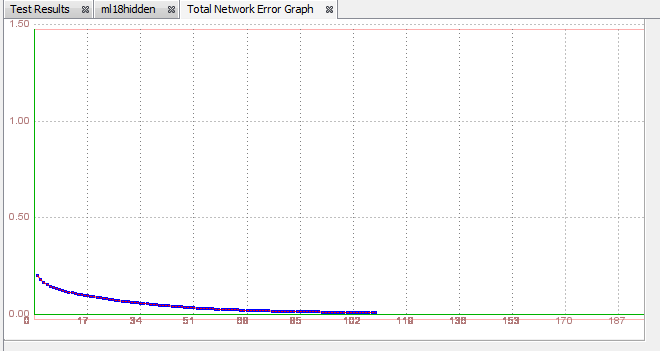
The error has became lower than 0.02 after 224 iterations and now we can start testing our network.
Testing the network After training, we click 'Test', to see if this set of parameters made the training better.It did! The total mean square error is lower, and the network made 30 wrong predictions.
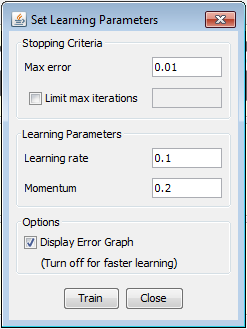
Training attempt 6Training and testing the network We will try to train the same 12 hidden neurons network with the different set of parameters - this time we will set the learning rate lower - to 0.1, and the momentum will stay the same - 0.7, max error will be 0.01. The error function minimum graph is shown below and the error minimum is found in iteration 185.
Training attempts 7 and 8Creating a neural network This solution will try to give same or better results as the previous one, with using more hidden neurons. The rule is to use only as little neurons as we can, but this time we will use 3 hidden neurons more so we can tell optimum number of them and to check is it really more better than less. We will create a new neural network, and set the number of hidden units to 15. All other parameters are the same as in the previous solution.
Training the network After creating it, we need to train the network. Now , we have 3 hidden neurons more than last time so for the first attempt we will use these parameters: for max error - 0.01, learning rate and momentum will be the same - 0.2 and 0.7. We click train and look at the error function graph.
After 152 iterations our new network is trained. We will now test it and see does it predict better than previous ones.
Testing the network After training the network, we click 'Test', so that we can how the well the network was trained. A tab showing the results will appear. We can see that the total error is 0.00225516, which is more than previous attempt ! Even number of extreme values of single errors is bigger than last time, 17 to 12. We can only say that this solution is not the best !
The last thing to do is to test the network again, but this time with the five inputs we randomly selected last time.The network guessed like previous one, 3 full guesses and other two were below 50%, but those misses were bigger than last time.We can conclude that this network is as good as the one with 12 hidden neurons, but little weaker. We will try one more time to train and test this network with 15 hidden neurons but now, we will change learning rate and momentum and error will be the same. Error function dropped below 0.01 after 121 iterations and we can test now is she trained properly.
After clicking on Test button we got these results :
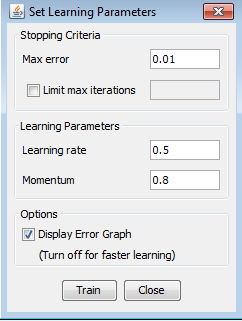
Mean square error is 0.0024675 and it had 19 individual errors, more than attempt 7 and attempt 6 so this time we won't test it with random inputs. Interesting conclusion this time: Although we added 3 more neurons we didnt get better results, so in our next and final 2 attempts we will try with more neurons to confirm or decline this assumption and we will set learning rate a little bit higher than we used to. Training attempts 9 and 10Creating and training the network As it is said above, now we will try to get better results with more hidden neurons or we will conclude that more doesnt need to mean better. Our final network will have 18 hidden neurons and for training we will set learning rate to 0.5, momentum to 0.8 and max error will be 0.01 so we can have the most accurate results.
We set parameters, training set and clicked Train. Error function graph shows us that these parameters are not adequate for network training. We couldn't train our network so we couldn't test it either. We need to change them so we can get some results.
We changed parameters for training so now we used these : leaning rate - 0.1 , momentum 0.2, max error - 0.01. Error function dropped below 0.01 after 278 as it is shown on graph. We can see a progress, our network is trained and all we need now is to test it.
Testing the network Will we get better results than in attempt 6, we will see after we do the network test. We managed to get lower mean square error ! Only 0.001763 ! It is a great result and we need now to see individual errors and to test it again with random inputs.
From 1003 instances we had 32 individual errors and 23 of them are bigger than 0.9. That is not good, but after random inputs test we can give conclusion. First input was ''Nothing in hand'' and we should get all zeros for a result. We got this : Second input was "Full house" and we should get value '1' on 6th place. We got this: Third input was "One pair" and the first value should be '1' and then 8 zeros. We got this: Fourth input was "One pair" and the first value should be '1' and then 8 zeros. We got this: Fifth input was "Royal flush and '1' had to be on 9th place in our result. We got this: Finally we got all five right guesses in five random cases. We can tell that this is well trained network and with attempt 6 (network with 12 hidden neurons) best solution.
Advanced training techniquesNext two attempts will be based on training our network with smaller training sets. First we will use only 20 % of our training set and then we will try to test our network with random inputs from other 80 %. In second attempt we will do reverse job : we will train our network with 80% training set and then test it with inputs from other 20% . If we manage to get good results we will be able to say that our network has power of generalization. Training attempt 11Creating a training set Now, we will try to change the training set used for the training of neural networks. Our training set which we used for all training and testing attempts, has 1003 instances. We will now only use 20% of those instances, and test whether the result will change. In other words, we will now test if a large number of rows is necessary to make a good data set. Procedure for creating training set is the same as last time. We have 85 inputs and 9 outputs. Only difference is that we are loading different file. That file has 200 instances. We will choose the network that gave the good results with the first training set - the network from the last training attempt 10. That neural network contains 18 hidden neurons in one hidden layer. We will now train that network with the newly created training set and observe whether the result will worsen or will they get better. Training the network Learning parameters are the same as last time : max error is 0.01 , learning rate is 0.1 an momentum is 0.2. Error has dropped below 0.01 after 169 iterations and we can test it now.
Testing the network We will find out if the result will be as good as the one made with first Training set. When the test results tab appears, we see that the total error is 0.002144. It is slightly bigger than 0.001763, the total error that training attempt 10 produced. This result has only 6 individual errors bigger than 0.5 and that is the best result we had, but we must test it with some random inputs to prove that this is the best solution.
After testing our network with 5 random inputs from other 80% of sample , we got this results:
We can see that our network couldn't guess all outputs , only 1 is correct. This proves that, while the result may appear better in the test result window, it is not true with real inputs. We will try to get better results with 80 % of training set.
Training attempt 12
Creating a training set The new training set will consist of 80% of the whole data set - 800 instances. We create this training set exactly the same as we did with the previous one,but this time we will load a file with 800 instances. After creating the training set, we choose an existing neural network from the training attempt 10 - the one that contains 15 hidden neurons. We will now train that network with the new training set. Training the network Learning parameters are the same as last time : max error is 0.01 , learning rate is 0.1 an momentum is 0.2.. Then, we click train and the iteration window will appear. This time, it stopped after 109 iterations.
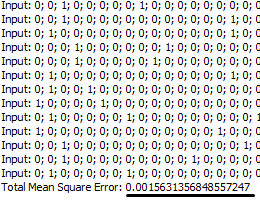
Testing the network The only thing left to do is to click 'Test' and test the network. Test results will show that the total mean square error is 0.001563. Network made 23 errors bigger than 0.3, which is around 3%. So far this network seems properly trained.
Now, it is time to test the network generalization ability. We will test it with inputs from other 20% that we didn't used in attempt. Here are the results:
We test the network with each of theese inputs. The results are shown in the table below: the network didn't guess all of them right. We can conclude that this network does not have a good ability of generalization so the training of this network can not be validated.
Conclusion Five different solutions tested in this experiment have shown that the choice of the number of hidden neurons is crucial to the effectiveness of a neural network. Other things that can have influence on our used networks are learning rate and momentum. We have concluded that more neurons does not mean that results will be better and that training and testing will be easier. When we set the learning rate and momentum to very low values , we had the best results, so that parameters must not be too high. Individual errors made for every input must be observed, only watching to total mean square error might mislead and get to some big errors in giving conclusions. In the end, after including only 20% of instances in the training set, we learned that that number can not be sufficient to make a good training set and a reasonably trained neural network and also neither we can with 80% of instances. Unfortunately , our networks does not have ability to generalize the problem. Below is a table that summarizes this experiment. The solutions which we could train for the problem are in bold.
See also:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


















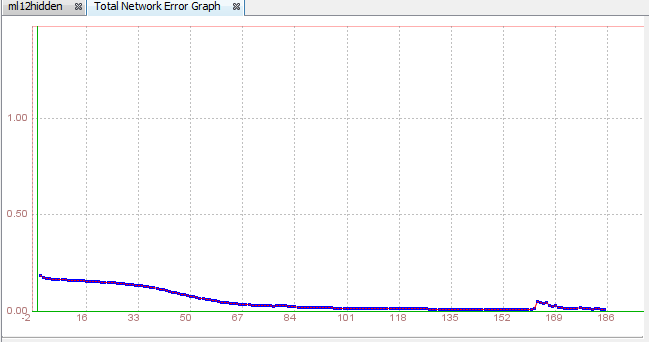
 → as we can see error is the lowest, only 0.00198
→ as we can see error is the lowest, only 0.00198